数え上げによる問題解決の事例

作田 誠

目次

1  数え上げによる問題解決の事例

1.1 算数パズル

※ 2004年大学センター試験「情報関係基礎」第2問から。図・設問・説明を引用。

数え上げ手法によりパズル問題 (一般的には小町算と言われるものの一種) を解く。

算数パズル問題

1 2 3 4 5 6 7 8 9 の順に数字を並べ、必要ならば各数字の左側に + または - を補って一つの計算式を作り、例えば

123-45-67+89

のように式の値が 100 になるものをすべて見つける。

「各数字の左側に + または - を補う」と考える代わりに「各数字の左側に、記号 + または - または □ (何もないことを表す) のうちの一つを配置する」と考える。 ただし、数字 1 の左だけは、+ は置かず - または □ (何もないことを表す) のうちの一つを配置する。

例えば、式 123-45-67+89 を図1のように考え、記号配置 (□, □, □, -, □, -, □, +, □) に対応させる。

図1  式と記号配置の例

処理手順の概要は図2のようになる。

図2  処理手順の概要


一つの記号配置を記録するのに配列 Kigo を用いる。 Kigo[i] には、数字 i の左側に配置した記号が - なら -1, □ なら 0, + なら 1 を記録する。

式 -1+2-3+4+5+6+78+9 の記号配置は (-, +, -, +, +, +, +, □, +) なので図3のように記録する。

図3  式 -1+2-3+4+5+6+78+9 に対応する Kigo の内容


次の空欄 [ア]・[イ] に入れるのに最も適当なものを下の解等群のうちから一つずつ選びなさい。


Kigo の内容が図4の場合、対応する式は [ア] である。

図4  Kigo の内容 (1)


Kigo の内容が図5の場合、対応する式は [イ] である。

図5  Kigo の内容 (2)


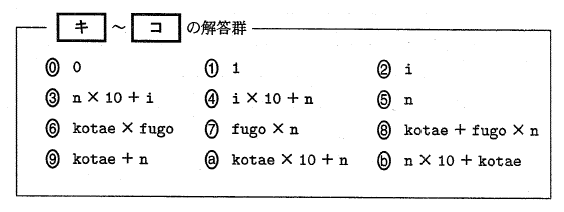
次の空欄 [ウ] ～ [カ] に入れるのに最も適当なものを、下のそれぞれの解等群のうちから一つずつ選びなさい。

Kigo の内容を図6のように変化させ、すべての記号配置を作る。 数字 1 の左には + を置かないので、Kigo[1] が -1 と 0 の記号配置だけを調べればよい。

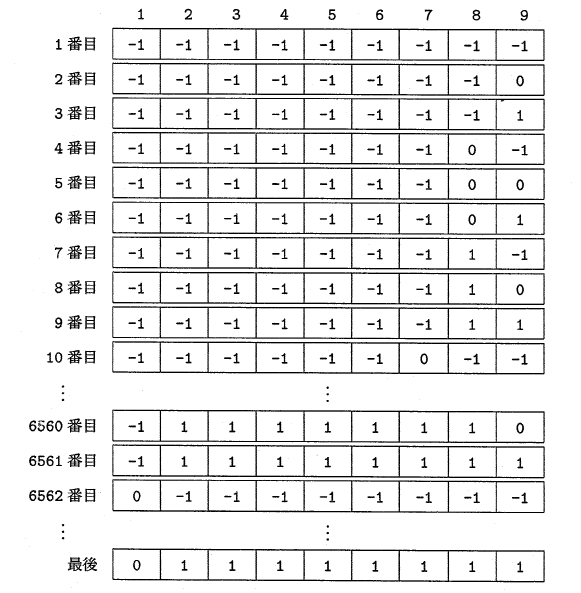図6  Kigo の変化の様子


図6の順に記号配置を作り出すために、図2の (A), (E), (F) の部分を詳しく書いた処理手順が図7である。
以下、(E-1)行のようなカンマで区切られた複数の代入文は左から右へ順に実行するものとする。例えば(E-1)行では、i ← 9 を行った後で Kigo[i] ← Kigo[i] + 1 を行う。

図7  
図2の(A), (E), (F) の部分を詳しく書いた処理手順


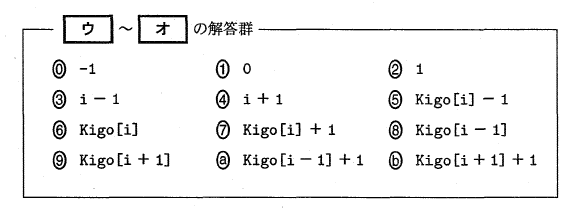
次の空欄 [キ] ～ [コ] に入れるのに最も適当なものを、下のそれぞれの解等群のうちから一つずつ選びなさい。ただし、同じものを複数回選んでも構わない。

図7の (C) の部分を詳しく書いた処理手順は図8のようになる。

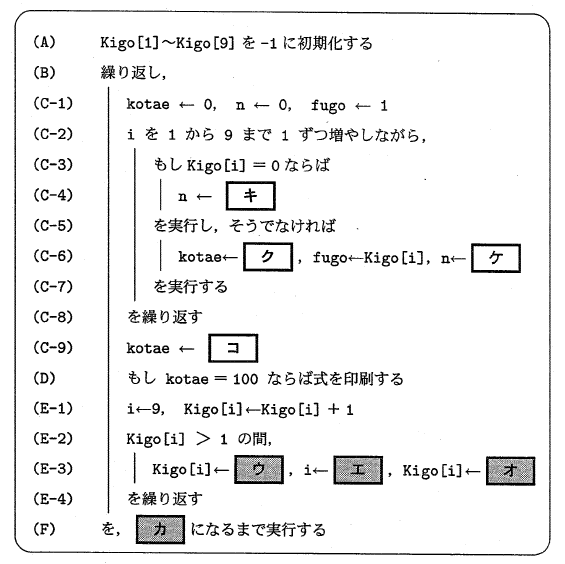図8  
図7の (C) の部分を詳しく書いた処理手順
[ウ] ～ [カ]は図7と同じ


変数の意味を表1に示す。

表1  変数の意味
変数意味
fugo式に含まれる数の +, -
n式に含まれる数
kotae式の値

123-45-67+89 という式は 123 + (-45) + (-67) + (+89) と考えることができる。 式の値を計算するには、式に含まれる数を次々に求め、それらの和を計算すればよい。

123-45-67+89 のとき、図8の (C-8) 行での変数 fugo, n, kotae の値は、変数 i の変化に伴って表2のように変化する。

表2  (C-8)行での変数の値の変化
変数値
i123456789
Kigo[i]000-10-1010
fugo111-1-1-1-111
n112123445667889
kotae00012312378781111


演習7
上の説明の空欄 [ア] ～ [コ] を埋めなさい。



演習8

上の説明の擬似コードにそって、このパズルの解答を出力するプログラムを作って実行し、各出力を確かめなさい。解の個数も求めること。

ただし、実行時にパラメータが指定されない場合は式の値が 100 になるものを解とし、パラメータとして整数値を指定した場合は式が指定された値になるものを解とすること。


※
独力でできない場合、

なお、両プログラムとも

(C言語) 
.\puzzle1to9   値

または

(Java) 
java   Puzzle1to9.java   値

のように「値」を指定して実行すると、100 以外の値の解を出力するようにしてある。

【注意】 試験問題の Kigo という変数は全部小文字の kigo に変更してある。

※

※※
[ア]から[コ]の解答
※※


演習9 降順小町算プログラムと出力

演習8のプログラムでは数字は 1, 2, ..., 9 の順に並べたが、今度は、演習8のプログラムをコピーして名前変更して修正し、逆に 9, 8, ..., 1 と並べた数字列の適当な箇所に +, - をつけた数式を作り、値が 100 になる数式を出力するプログラムを作りなさい。解の個数も求めること。

ただし、実行時にパラメータが指定されない場合は式の値が 100 になるものを解とし、パラメータとして整数値を指定した場合は式が指定された値になるものを解とすること。



課題4 小町算 (一般課題)

テキストファイル (拡張子 txt) に、以下を順にまとめなさい。

まとめたテキストファイルを授業Webページの課題提出のところから提出。


ここまでの問題解決手法は、「問題の終端状態が容易に数え上げることができる場合」の非常に効率的な解法であった。
より一般的には、再帰を使った深さ優先探索を用いて各終端状態まで探索し、解に合致するものを数え上げる手法を使う。

1.2 再帰を使った数え上げ

一般的な手法で、再帰を使った数え上げを行うためには、「数え上げ・探索の手法」のリスト「数え上げの再帰的記述」で示した擬似コードを使えばよい。

そのためには、対象とする問題における数え上げあるいは探索中の一過程を完全に表現するものとして

「状態」をひとまとまりの形 (C言語なら構造体、C++やJavaならクラス) で表現する

とよい。そして、その「状態」に対し、

  • すべての可能選択肢を求める
  • ある選択肢を選び進める
  • 選んだ選択肢から元の状態に戻る

という3つの手続き (C言語なら「状態」構造体を指すポインタを引数とする関数、C++やJavaなら「状態」クラスのメソッド) を用意する

必要がある。ただし、実装の仕方によっては「選んだ選択肢から元の状態に戻る」手続きは不要の場合もある。
適用する問題に応じ、その他の手続きも用意する。


※ 以下は、余裕がある人のための発展課題である。一般に科目合格を目指すだけならばやらなくてよい。


課題5 昇順小町算の再帰による数え上げ (任意提出・発展課題)

演習8を、 「数え上げ・探索の手法」のリスト「数え上げの再帰的記述」に示した擬似コードを参考にプログラミングしなさい。
ソースプログラムと実行結果の出力をテキストファイル (拡張子 txt) にまとめ、Webから提出しなさい。


この課題をこなすためには、プログラムで数式の設定状態を表現し、

を用意し、「数え上げ・探索の手法」のリスト「数え上げの再帰的記述」を少し書き換えた以下のような擬似コードを実装すればよい。

リスト1  小町算の解数え上げの再帰的記述

数え上げ (状態) {
    「状態」でのすべての可能選択肢を求める
    選択肢がない (= 末端状態) ならば
        数式を評価し値を求める
        値が目的値なら、数式を表示
        戻る
    すべての可能選択肢について {
        次の数字を選択肢で接続する
        数え上げ( 状態 )
        最後に接続した数字を切り離す
    }
}