探索による問題解決の事例

1.1 N-Queen問題

チェスに縦横ナナメに長く移動できるQueenという駒がある。Queenの動きは図1を参照。

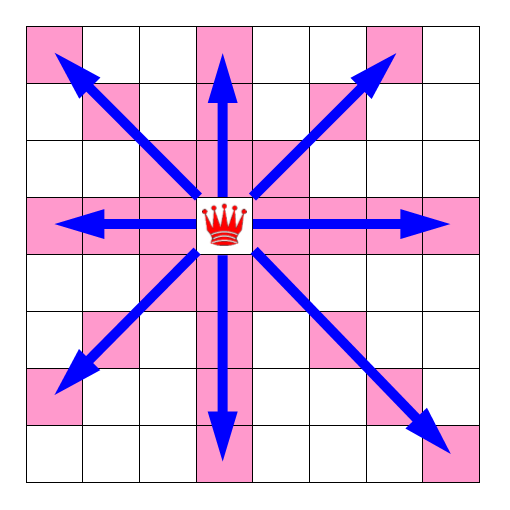図1  Queenの可能な動き

N-Queen問題 (N-Queens Problem) とは、縦横 N 個 × N 個 のマスからなるボードに、N 個のチェスのクイーン駒を相互に利きがぶつからないように配置する問題で、チェス盤に8個のクイーンを配置する8-Queen問題の一般化されたものである。

図2に N = 7 のときの解答の一つを示す。

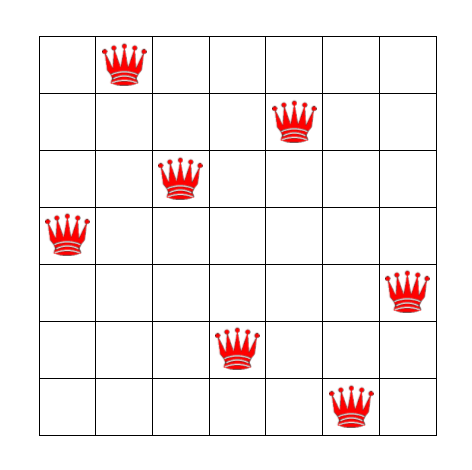図2  N-Queen問題で N = 7 のときの一解答

本来はすべての配置を数え上げる問題で、探索量が指数関数的に爆発するため現在でも N = 30 近くが限界となっている。

今回の問題では、最初は、設定を「1個でも配置を見つければよい」探索問題とする。
後で、すべての配置を数え上げる問題も対応する。

※ 実は、解を1個求めるだけなら、探索をせず、特定の規則でQueenを置いていくだけで解が生成できることが知られている。後の節を参照のこと。

今回の問題を解くために、まず固定サイズの際の素朴な探索アルゴリズムを考え、次に、サイズを変更可能とするため、再帰 (recursion) を用いた深さ優先探索を適用する。

1.2 基本的手法と素朴なアルゴリズム

まず、問題解決のための基本的手法を考える。
N-Queen問題の解には

• クイーンは必ず各列に一個
• クイーンは必ず各行に一個
• ナナメ右上あるいは右下方向には、クイーンがないか、もしくは一個ある

という特徴がある。 これから、

左(０列目)の列から順に右に、
        列のうちのクイーンを置けるマスのどこか
        (上のマスから順に試す)に配置してゆく。
列にクイーンが置けなくなったら
        一つ前の列に戻って、別のマスを試す。
        もう試すマスがないときは、さらにもう一つ前の列に戻る。
全部のクイーンが配置できたら終了。

という手順が考えられる。

探索の様子がわかるプログラム NQueenSearch.jarをTeams授業チーム「ファイル」の下の NQueen フォルダに置いてあるので、実行して色々試してみるとよい。 ダウンロードし、PowerShell またはコマンドプロンプトを起動し、ファイルを置いてあるフォルダに cd で移動した後、

というコマンドでプログラムが起動できる。

いきなり問題を一般化して解くのではなく、まずはクイーンの数の小さい問題で考えてみるとよい。
4-Queen問題について、実際に順番に配置をして調べていく動作を素朴に記述してみる。

０列目のすべてのマスについて {
        クイーンを置く
        一列目のすべてのマスについて {
                置けるマスならば {
                        クイーンを置く
                        二列目のすべてのマスについて {
                                置けるマスならば {
                                        クイーンを置く
                                        三列目のすべてのマスについて {
                                                置けるマスならば {
                                                        クイーンを置く
                                                        解を見つけた。表示し終了
                                                }
                                        }
                                        置いたクイーンを戻す
                                }
                        }
                        置いたクイーンを戻す
                }
        }
        置いたクイーンを戻す
}

1.3 データ表現とサポート処理群

プログラムのデータ表現を考える。

ボードの大きさ(=クイーンの数)は値を変更できるよう変数 (boardSize とする) で表す。

Java では

ボードのデータを boardSize × boardSize の二次元配列 (boardData とする) で表し、

static final int DEFAULT_BOARD_SIZE = 8; // ボードの大きさ(=クイーンの数)のデフォルト値
int boardSize = DEFAULT_BOARD_SIZE;
boolean[][] boardData = new boolean[boardSize][boardSize];

のように記述できる。上記のように boardData 配列を new で確保した場合、配列のすべての要素が false で初期化されている。

ボード上の行と列を 0 から始め (boardSize - 1) までとし、行は上が 0 で下に行くに従い増加、列は左が 0 で右に行くに従い増加するとする。 ボード上 i行j列 のマスのデータが boardData[i][j] で表されるとする。

boardData[i][j] が

ことを表す。

C言語では

ボードのデータを 最大サイズ × 最大サイズ の二次元配列 (boardData とする) で表し、

#define MAX_BOARD_SIZE 40 /* ボードの大きさ(=クイーンの数)の最大値 */
const int DEFAULT_BOARD_SIZE = 8; /* ボードの大きさ(=クイーンの数)のデフォルト値 */
int boardSize = DEFAULT_BOARD_SIZE;
unsigned char boardData[MAX_BOARD_SIZE][MAX_BOARD_SIZE];

のように記述できる。

先頭付近で

#include <stdbool.h>

として標準ヘッダをインクルードする (C99 準拠のコンパイラの場合) か、あるいは

#define true 1
#define false 0

と定義しておけば、C言語でも false, true を使用できる。

C言語で、関数の外部でグローバルに boardData 配列を定義した場合、すべての要素が 0 で初期化されており、false とみなせる。

次に、マスにクイーンが置けるかどうかをチェックするため、

• ある行にクイーンが置かれているかどうかを示す一次元配列 (rowPlaced とする)
• 左上斜め方向にクイーンが置かれているかどうかを示す一次元配列 (diagNWPlaced とする)
• 左下斜め方向にクイーンが置かれているかどうかを示す一次元配列 (diagSWPlaced とする)

を用意する。

Java では

boolean[] rowPlaced = new boolean[boardSize];
boolean[] diagNWPlaced = new boolean[2*boardSize - 1];
boolean[] diagSWPlaced = new boolean[2*boardSize - 1];

のように記述できる。
rowPlaced, diagNWPlaced, diagSWPlaced 各配列を上記のように new で確保すると、配列のすべての要素が false で初期化されている。

C言語では

unsigned rowPlaced[MAX_BOARD_SIZE];
unsigned diagNWPlaced[2*MAX_BOARD_SIZE - 1];
unsigned diagSWPlaced[2*MAX_BOARD_SIZE - 1];

のように記述できる。関数の外部で配列を定義した場合、配列のすべての要素が 0 で初期化されており、false とみなせる。

リスト2のアルゴリズムを記述する上で必要になる細かい処理を以下に示す。

ボードデータの初期化

ボードのデータをすべて空とする
(boardData, rowPlaced, diagNWPlaced, diagSWPlaced 各配列のすべての要素を false にする。)
※ Java では、new で boolean 配列を確保すると各要素は false で初期化されるので、プログラムが一回しか問題を解かないのであれば不要。
※ C 言語では、関数の外あるいはstaticな変数として宣言した場合、プログラムが一回しか問題を解かないのであれば不要。

クイーンを置く、置いたクイーンを戻す、置けるかどうかのチェック

クイーンを i行j列 に置く {
	boardData[i][j] = true
	rowPlaced[i] = true
	diagNWPlaced[i - j + boardSize - 1] = true
	diagSWPlaced[i + j] = true
}

クイーンをある列に置くと、その右側の列の以下のマスにはもうクイーンは置けない。

そのクイーンを置いた行のマス	⇒	rowPlaced[i] = true で表す
そのクイーンを置いたマスのナナメ右下方向にあるマス	⇒	diagNWPlaced[i - j + boardSize - 1] = true で表す
そのクイーンを置いたマスのナナメ右上方向にあるマス	⇒	diagSWPlaced[i + j] = true で表す

i行j列 に置いたクイーンを戻す {
	boardData[i][j] = false
	rowPlaced[i] = false
	diagNWPlaced[i - j + boardSize - 1] = false
	diagSWPlaced[i + j] = false
}

ある列にクイーンを取り去ると、その右側の列の以下のマスにはクイーンが置けるようになる。

そのクイーンを置いた行のマス	⇒	rowPlaced[i] = false で表す
そのクイーンを置いたマスのナナメ右下方向にあるマス	⇒	diagNWPlaced[i - j + boardSize - 1] = false で表す
そのクイーンを置いたマスのナナメ右上方向にあるマス	⇒	diagSWPlaced[i + j] = false で表す

i行j列 にクイーンが置けるかどうかのチェック {
(ただし、j列以降にはクイーンはまだ置かれていない状態)
	「rowPlaced[i] が false」
		かつ「diagNWPlaced[i - j + boardSize - 1] が false」
		かつ「diagSWPlaced[i + j] が false」
	であればOKなので true を返す。
	それ以外はNGなので false を返す。
}

該当マスの行のマス、該当マスのナナメ右下・右上方向のマス、すべてにクイーンがまだ置かれていなければ、そのマスにはクイーンが置ける。そうでなければ置けない。

1.4 再帰を使ったアルゴリズム

リスト2の方法は、無駄にループが深くなり、クイーンの数の変化に対応できない、という問題点がある。そこでリスト2のアルゴリズムを参考に、再帰呼び出しを使ったスマートなコードに書き換えてみる。

問題解決をする手続き search メソッド (関数) が呼び出されると、searchSub メソッド (関数) が呼び出される。実際に再帰しているのは searchSub メソッド (関数) である。

整数型 search() {
	r = searchSub( boardSize )
	r を返り値として呼び出し元に戻る
}

整数型 searchSub( n ) {  // n は未配置クイーンの残り枚数
	n1 = n - 1   // n1 は次の段階での未配置クイーンの残り枚数
	(boardSize - n)列目のすべての行iのマスについて {
	    置けるマスならば {
	        クイーンを i行(boardSize - n)列 に置く
	        n1 が 0 なら {
	                配置成功なので、1 を返り値として呼び出し元に戻る
	        }
	        r = searchSub( n1 )
	        r が 0 でなければ {
	                配置が見つかったので、r を返り値として呼び出し元に戻る
	        }
	        i行(boardSize - n)列 に置いたクイーンを戻す
	    }
	}
	配置失敗。0 を返り値として呼び出し元に戻る
}

プログラムの中で

        r = search()

のように search メソッド (関数) を呼び出し返り値を整数型の変数 r に代入すれば答を見つけることができる。
返り値 r が 0 でなければ配置が見つかったので、解を出力すればよい。返り値 r が 0 のときは解が存在しないことが保証される。

1.5 解の総数を求めるプログラム

前述したように、本来のN-Queen問題は解の総数を求める問題である。 ちなみに小さい N と解の総数の対応を表1に示す。

※ 下は回転や反転で同一となる配置も複数のままとして求めた総数である。対称性を考慮した場合の重複のない解の数は下表よりもかなり少ない。

リスト3のコードを少し変更して、searchSubで見つかった解の個数を返すようにする。例えば、以下のような擬似コードになる。

整数型 searchSub( n ) {
    // n は未配置クイーンの残り枚数を表す
    n1 = n - 1
    n1 が 0 なら {
            整数型 count = 0
            (boardSize - 1)列目のすべての行iのマスについて {
                    置けるマスならば {
                            // 配置成功 (解を一つ見つけた)
                            count に 1 加える
                    }
            }
            // 見つかった解の数を返す
            count を返り値として呼び出し元に戻る
    }

    // 以下は n1 > 0 のとき

    整数型 count = 0
    (boardSize - n)列目のすべての行iのマスについて {
            置けるマスならば {
                    クイーンを i行(boardSize - n)列 に置く
                    整数型 r = searchSub( n1 )
                    count に r を加える
                    i行(boardSize - n)列 に置いたクイーンを戻す
            }
    }
    // 見つかった解の数を返す
    count を返り値として呼び出し元に戻る
}

1.6 ボード配列を使わない方法

まず、探索版プログラムの変更について説明する。

今まで説明したN-Queen問題解答プログラムでは、ボードデータの表現として

サイズ boardSize × boardSize の二次元配列 (boardData とする) で表し、

という形式を使っている。

しかし、N-Queen問題の解では各列 (または各行) に必ず一個のQueenが配置されるという条件が成立するため、ボードを表す配列を使わず、一次元配列 rowPlaced を各行の何列目にクイーンが置かれているかを表すように変えるとボードデータを表現できる。ボード配列を使ったときと比べ、少なくとも使用メモリ量を削減でき、また実行速度アップも期待できる。
※ 実際の実行速度には、より複雑な複数の要因が関係するため、今回の変更で必ずしも速くなるとは限らない。

この表現では、rowPlaced 配列の意味を変えて

という形式にすればよい。

このとき、上記の変更に伴い、以下の変更をプログラムに加える必要がある。

変数定義部分で、boardDataの削除とrowPlacedの型を int 配列に変更

ソースにある boardData 定義の行は削除する。

rowPlaced は int 型の配列に変更する。

ボードデータの初期化

boardData配列の初期化用コードはすべて削除する。

rowPlaced配列のインデックス 0 〜 boardSize - 1 までのすべての要素を -1 にする。(初期化必須)
diagNWPlaced, diagSWPlaced 各配列については前と同様。

※ 雛形ソースを基にしている場合は、setBoardSize 関数 (メソッド) に変更を加えること。

クイーンを i行j列 に置く

boardDataに関するコードは削除する。

	rowPlaced[i] = j

diagNWPlaced, diagSWPlaced 各配列の更新については前と同様。

i行j列 に置いたクイーンを戻す

boardDataに関するコードは削除する。

	rowPlaced[i] = -1

diagNWPlaced, diagSWPlaced 各配列の更新については前と同様。

i行j列 にクイーンが置けるかどうかのチェック

「rowPlaced[i] が false」をチェックしている部分を以下のように rowPlaced[i] がマイナスであるかどうかをチェックするように変更する。

	rowPlaced[i] < 0

diagNWPlaced, diagSWPlaced 各配列のチェックについては前と同様。

解を表示する関数 (メソッド) printSolution (雛形ソースを基にしている場合) 内の修正

	if ( boardData[i][j] ) {

の行を

	if ( rowPlaced[i] == j ) {

に変更。

次に、解の総数を数えるプログラムの変更について説明する。
このプログラムでは、解のボード図を表示しないので、そもそも完全なボード状態を持っている必要はない。
単純に boardData に関わる部分をすべて削除すればよい。
解を表示する関数 (メソッド) printSolution (雛形ソースを基にしている場合) も削除する。

以上の変更を加えて、探索プログラムおよび解の総数を数えるプログラム両方を書き換え動作させる。

1.7 特定規則による解の生成

N-Queenの解を1個求めるだけであれば、解を生成する特定規則が知られている。
行および列のインデックスを 0 オリジンで記述すると下記の手順となる。