1 ニューラルネットワーク
ニューラルネットワーク (neural network) あるいは 人工ニューラルネットワーク (artificial neural network) は、神経細胞の働きを単純化しモデル化することによって生まれた機械学習の一手法である。
1.1 概要
ニューラルネットワークにはいくつか種類があるが、この講義では広い分野で応用され成功を収めている 順伝播型ニューラルネットワーク (feed-forward neural network) について触れる。
順伝播型ニューラルネットワークでは、ネットワークにループする結合を持たず、値を保持する複数のノードから構成された 層 (layer) を重ねた構造となっている。信号は、
というように単一方向にのみ伝播していく。これを、方向を意識して示す場合は 順伝播 と言う。
i層の値をベクトル Xi で表すと、一般的には下記の式で表現できる。
Ai は重みパラメータの行列
Bi はバイアス値を表すベクトル
fi は 活性化関数 (activation function)
である。
※ Ai と Bi を合せ拡張行列 Wi で表現すれば、
となる。一般的には、バイアスも含めた Wi を 重み weight と言う場合が多い。
多層のニューラルネットワークの中で k-1 層から k 層への信号の順伝播を、k 層の 1 ノードに注目した場合の計算の様子を下図に示す。
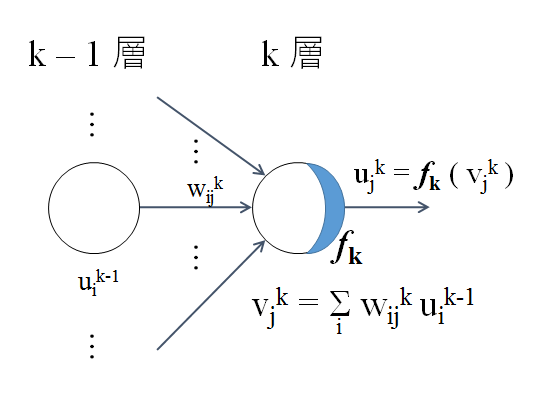
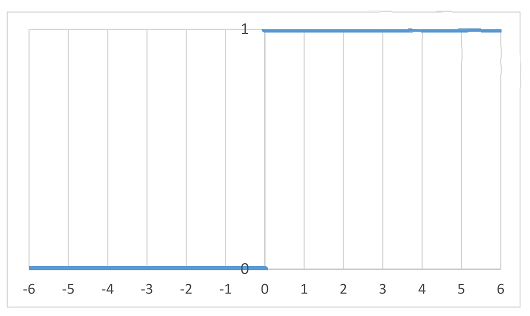
活性化関数が f(x) = ax + b のような線形関数だと、ニューラルネットワーク全体でも線形関係しか表現できないが、活性化関数を シグモイド 1/(1 + e-x) といった非線形関数にして層やノードの数を増やせばニューラルネットワーク全体での表現能力をどれだけでも高められることが分かっている。ただし、構成を複雑にすればするほど、パラメータの数も増大し、パラメータ調整は困難になる。
重みパラメータの調整には、逆伝播 (backpropagation) を用いる。一般に、入力からネットワークを通して得られる出力値群と訓練データの目標値群とのズレを 損失関数 (loss function) で表す。最初は、出力層において、損失関数の 勾配 (gradient) (偏微分値のベクトル) を逆方向に伝播させる。なお、一般に、勾配の要素 (偏微分値) が「出力値と目標値との差」になるように損失関数を設定する。
出力層以外では、逆伝播してくる偏微分値に重みの値を掛け足し合わせ、合計値を求める。
その合計値と活性化関数の微分値を掛け合わせ、各ノードのデルタ値 (勾配) を求める。求めたデルタ値をさらに前の層に逆伝播させていく。
この逆伝播を出力層から始め入力層に達するまで行なう。
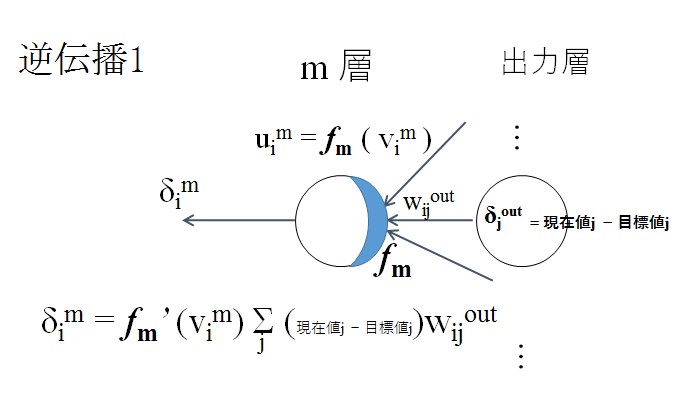
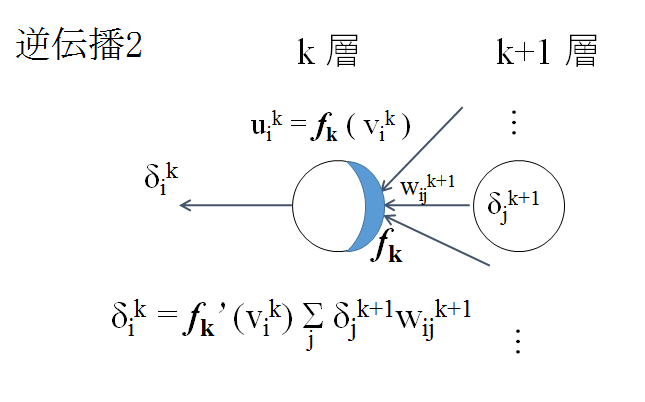
このような逆伝播で、各ノードのデルタ値 (勾配) が求まる。これを基に重みパラメータの更新を行なう。

各ノードの勾配は訓練データとのズレを表しており、損失関数の値を小さくするためには、ネットワーク上の各ノードのパラメータを勾配と逆方向に動かしていけば段々とズレが小さくなっていくことが期待される。単純に、デルタ分 (ひとつ前の層のノード値と今の層のノードの偏微分値との積) に対して 学習率 (learning rate) α という小さい値を乗じて元の重みパラメータ値から差し引く手法が古くから使われており、勾配降下法 (gradient descent) (または 最急降下法) と言われる。
勾配降下法にも、パラメータの更新を行うデータの個数によって以下の種類がある。
- (バッチ)勾配降下法
- 訓練データセット全体の勾配の和を求めて重みパラメータの更新を行う。
- 確率的勾配降下法 (stochastic gradient descent, SGD)
- ランダムに選んだ訓練データ1個ごとに勾配を求めて重みパラメータの更新を行う。個々のデータに対する変更を累積していくことによって、十分な確率で訓練データ全体に対して望ましいパラメータが得られていくことを期待している。
局所解 (ローカルミニマム) に陥りにくいという利点があるとされる。 - ミニバッチ勾配降下法
- 訓練データから決まった個数ごとをランダムに選び、それらの勾配の和を求めて重みパラメータの更新を行う。
この中でも、実装が容易で学習性能もそれほど悪くない SGD が従来からよく用いられてきた。
一般に、機械学習によって重みパラメータを調整し損失関数の値を最小化していくことを 最適化 (optimization) という。 最適化には、初期のニューラルネット応用では単純な SGD 法が使用されていたが、最近はパラメータの変化履歴を考慮して効率化を図った洗練された数種の手法 (RMSprop, Adadelta, Adam など) も使用されている。
順伝播型ニューラルネットワークの利用として、下の2通りの用途が挙げられる。
- 分類 (classification) (2クラス分類または多クラス分類)
入力データを、何らかの特徴をもった複数のクラスのうちの一つに分類する。
- 回帰 (regression)
入力データから出力を推定できるようにする。多次元入力・多次元出力の関数の近似と考えることができる。
一般に、損失関数として、分類問題では 交差エントロピー (cross entropy)
pi は i 番目の出力値 (i 番目に分類される確率)、ti は訓練データの分類における i 番目の値
が、回帰問題では 平均二乗誤差 (mean squared error) に比例した
yi は i 番目の出力値、ti は訓練データの i 番目の値
が使用される。これらの損失関数を使うと、出力層の勾配の要素 (偏微分値) が
という単純な形で表せ、逆伝播のとき都合がよいためである。(ただし、分類問題では出力層の softmax 活性化関数も含めた勾配が上記の式となる)
初期には、層i と 層i+1 の間で、層i のすべてのノードに対して 層i+1 のすべてのノードに対する重みパラメータを考慮する形 (全結合層 fully-connected layer または dense layer と言われる) ですべての層を構築したネットワークが利用されていたが、
- パラメータが多くなりすぎて学習が困難になる
- 問題に特化した形で特徴量を使えない
などの問題があり、ニューラルネットワークは余り成果をあげられなかった。
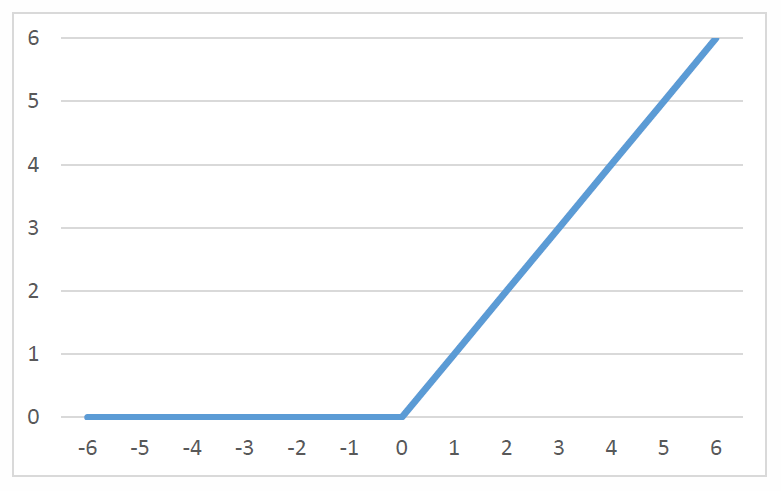
しかし、画像認識の分野で2次元画像を2次元のまま見て、小さい矩形に分割しその中でのみ結合を考える層 (畳み込み層 convolution layer) を入れた 畳み込みニューラルネットワーク (convolutional neural network) が成功し、さらに、活性化関数に単純な
f(x) = max(0, x)
= 0 (x <= 0 のとき), x (x > 0 のとき)
等を使用し、かなり多層にした構造のネットワークが画像認識を高い精度でできることが示され一気に普及した。
1.2 ごく小さいネットワークでの計算例
2入力・2出力の回帰問題について、以下のニューラルネットワークを考える。
入力は2個の数値、ノード2個の中間層1層 (活性化関数 f は ReLU)、ノード2個の出力層 (活性化関数はなし) からなるごく小さいネットワークとする。
下図のように、入力から中間層への重みパラメータを
中間層から出力層への重みパラメータを
とする。ただし、b00, b01, c00, c01 はバイアス値である。
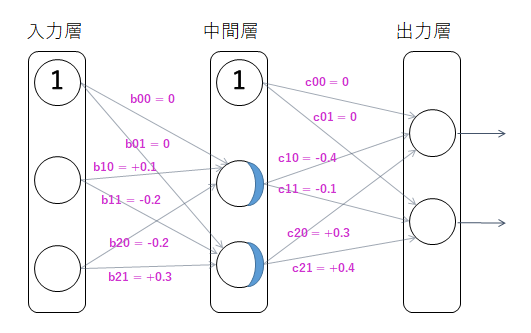
初期値として、以下の値になっているとする。
ここで訓練データとして入力 X = (1, 1) 出力 Y = (1, 0) を与え、学習率 α = 0.1 とした SGD によりパラメータを更新する。
まず、順伝播をみる。中間層の中央のノードは
となり、活性化関数 ReLU を f で表すとすると、
となる。中間層の一番下のノードは
u = f(v) = f(+0.1) = +0.1
となる。出力層の上の方のノードは
となる。出力層の下の方のノードは
となる。以上で、下図のように値が設定される。

次に、逆伝播をみていく。まず各ノードのδ値を求めていく。出力層において出力 (+0.03, +0.04) と教師値 (1, 0) との差は、上のノードで
下のノードで
となる。中間層の中央のノードでは、
となるが、
となる。ここで、ランプ関数 ReLU の微分 として以下を使っている。
※ x = 0 のときは微分が定義できないので、ここでは f'(0) = 0 とする。
ノードの値が 0 のときは微分が伝播しないので影響はない。
中間層の一番下のノードでは、
となり、
となる。以上で、δ値は下図のように設定される。

次に、重みパラメータの更新を行う。まず、中間層・出力層間の重みの変化をみる。
バイアスの値は
c01 = c01 - αδu = 0 - 0.1 * (+0.04) * 1 = -0.004
となる。c10, c11 については、中間層の中央のノードは u=0 のため、重みパラメータの値は変化しない。
中間層の一番下のノードの u=+0.1 は 0 でないため、重みの値が更新され、
c21 = +0.4 - 0.1 * (+0.04) * (+0.1) = +0.3996
となる。
次に入力と中間層間の重みの変化をみる。
b00 については中間層の中央のノードが δ=0 のため値は変化しないが、 b01 は
となる。
また、b10 の値は変化しないが、b11 は
となる。同様に、b20 の値は変化しないが、b21 は
となる。以上で、重みパラメータは下図のように更新される。
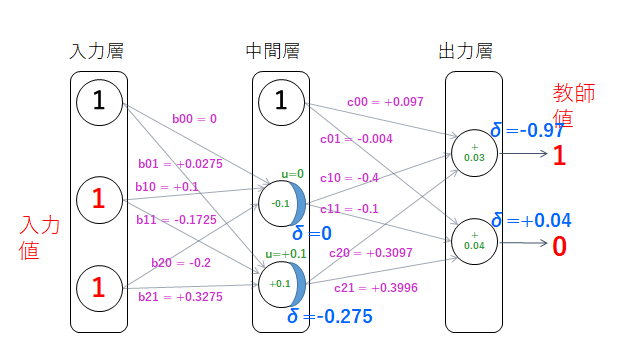
なお、更新後の重みパラメータを使って入力 X = (1, 1) の場合の出力 Y は以下のように計算される。
v = 0 + 1 * (+0.1) + 1 * (-0.2) = -0.1
u = f(v) = 0
中間層の一番下のノード
v = +0.0275 + 1 * (-0.1725) + 1 * (+0.3275) = 0.1825
u = f(v) = 0.1825
出力層の上ノード
v = +0.097 + 0 * (-0.4) + 0.1825 * (+0.3097) = 0.15352025
出力層の下ノード
v = -0.004 + 0 * (-0.1) + 0.1825 * (+0.3996) = 0.068927
上記計算から 出力 Y は学習前の (+0.03, +0.04) から Y = (+0.15352025, +0.068927) に変わる。教師値 (1, 0) に対し、上ノードは約 0.12 近づいているが、下ノードは逆に約 0.03 遠ざかったことがわかる。
このように、1個の訓練データを1回適用するだけでは、学習はほとんど進まず偏った結果に導かれてしまう。実際の学習では多数の訓練データを多数回適用する必要がある。
以下のPowerPointファイルとソースファイルを、zipファイル (拡張子 .zip) としてまとめて、授業Webページから提出しなさい。
1. 下記 (A) (B) を PowerPointファイル (拡張子 .pptx) にまとめる。
PowerPoint最初のページに「学籍番号・氏名」と「課題番号 課題名」。その後 (A), (B) のページを続ける。
(A)
- 上例で、さらに2個目以降の訓練データとして以下を順に与え学習率 α = 0.1 とした SGD によりパラメータを更新していく場合の重みパラメータの変化を、順に、上例のようなニューラルネットワーク図の上に示しなさい。
- 入力 X = (1, 0) 出力 Y = (0, 1)
- 入力 X = (0, 1) 出力 Y = (0, 1)
- 入力 X = (0, 0) 出力 Y = (0, 0)
(B)
- 上例の訓練データを含め、4個の訓練データをあたえて訓練した後、重みパラメータを固定して出力をみる。以下を順に与えた場合の出力を順にニューラルネットワーク図の上に示し、訓練データとの差を調べなさい。
- 入力 X = (1, 1)
- 入力 X = (1, 0)
- 入力 X = (0, 1)
- 入力 X = (0, 0)
2. 上例および上記 (A), (B) のニューラルネットワークの構造と学習の様子を逐次確認できるC言語またはJavaで記述されたプログラムのソースファイル (拡張子 .c または .java)。提出ソースファイルだけで完全動作するものとすること。
2入力・1出力の回帰問題について、以下のニューラルネットワークを考える。
入力は2個の数値、ノード2個の中間層1層 (活性化関数 f は ReLU)、ノード1個の出力層 (活性化関数はなし) からなるごく小さいネットワークとする。
下図のように、入力から中間層への重みパラメータを
中間層から出力層への重みパラメータを
とする。ただし、b00, b01, c00 はバイアス値である。

初期値として、以下の値になっているとする。
ここで訓練データとして入力
を与え、
とした SGD によりパラメータを更新する。
- 順伝播を計算し、中間層ノードの v1, u1 (活性化関数 f 適用後), v2, u2 (活性化関数 f 適用後) および出力層の v を、計算式を示し求めなさい。
v1 =
u1 =
v2 =
u2 =
v = - 逆伝播を計算し、出力層のデルタ値 δ および中間層のデルタ値 δ1, δ2 を、計算式を示し求めなさい。
δ =
δ1 =
δ2 = - 逆伝播に伴う重みパラメータ更新を計算し、各パラメータの値を示しなさい。ただし、値が変わるものについては計算式を示して求めなさい。
b00 =
b01 =
b10 =
b11 =
b20 =
b21 =
c00 =
c10 =
c20 = - 重みパラメータ更新後、入力 (0,1) に対する順伝播を計算し、v1, u1, v2, u2 および v を、計算式を示し求めなさい。
v1 =
u1 =
v2 =
u2 =
v =
テキストファイル (拡張子 txt) に、
先頭に「学籍番号・氏名」と「課題番号 課題名」
を入れ、その後に上記の全問について計算式と結果を入れて保存し、授業Webページから提出。
1.3 畳み込みニューラルネットワークの基礎と深層学習
初期の順伝播型ニューラルネットワークは、ひとつ前の層の全ノードと後の層の全ノードの全ての組合せに対して結合を考え重みパラメータを用意し調整する、いわゆる 全結合層 のみから成るネットワークであった。
全結合のとき、層kのノード数が m 個、層(k+1)のノード数が n 個としてバイアスも考慮すると、層k - 層(k+1)間の重みパラメータの数は
となる。
従って、例えば 1000 ノード同士の層の間には 百万 を超える重みパラメータが必要となるなど、複雑なモデルに対してパラメータ数の増加が顕著で、その分パラメータ調整が困難になってくる。
ここで、画像データなど、入力のノード群が意味のある位置関係を持っている場合に、ノード間の位置関係の情報を維持したまま次の層にデータを渡していくと、元データの特徴を学習に活かすことができる。
これを実現するのが畳み込み層 (convolution layer) で、典型的には、2次元データを2次元のまま見て、小さい矩形に分割しその中でのみ結合を考える。
なお、畳み込みは2次元データに対して行われることが最も多いが、ノード間の位置関係次第で、1次元構造のデータや3次元構造のデータに対して畳み込みを行うこともできる。
一般に、畳み込み層を持ったニューラルネットワークのことを 畳み込みニューラルネットワーク (convolutional neural network : CNN) と言う。
畳み込み層は全結合層に比べパラメータ数が非常に少なくて済むので計算が効率化でき、その結果多層化でき、また、元データの特徴を生かせる利点もあり、画像の認識で従来法に比べて非常に高い精度を示すことができるようになった。
2次元畳み込みでは、カーネル (kernel) もしくは フィルター (filter) という小さな矩形パラメータ領域を使い、対象となっている層の2次元データの左上端からカーネルを適用し、対象層データとカーネルのデータ値の積の総和を求め、さらに総和に バイアス (bias) 値を加算し、必要なら総和に活性化関数を適用し、次の層の左上端のノード値とする。 カーネルは左上端から右にずらしていき、次層の上端右側のノード値を設定していく。カーネルが対象層データの右端に達したら、次は、上端より一個下の左端にずらして、その位置の次層のノード値を計算する。 以下同じようにカーネルを右に・下にずらしていき、その位置の次層のノード値を計算していく。カーネルが右下端に達したら終了となる。
右・下にずらす量は ストライド (stride) と言われ、標準では (1,1)、すなわち、右にも下にも1つずつずらしていく。これより大きいストライドを使って、もっとまばらな要素を使う畳み込みを行うこともできる。
2次元畳み込みのカーネルは、典型的には、3×3 や 5×5 などのサイズが使われるが、2×2 のように偶数を使うこともできるし、意味があれば 3×4 のような正方形でないものも使用することができる。ただし、偶数サイズを使うと中心がデータ位置と合わないので画像データに対してうまく働かない可能性があると言われている。
CNNでは、畳み込み処理と合わせ、データサイズを縮小する プーリング (pooling) という処理が多くのケースで利用される。プーリングには数方式があるが、簡単なものでは、データの局所的な矩形領域の最大値を代表値として採用する 最大値プーリング (max pooling) があり、多く使用されている。他には、領域のデータの平均値を代表値とする 平均プーリング (average pooling) もある。
1.3.1 畳み込み、プーリングのごく簡単な例と演習
CNNの途中の層が以下で示す 6×4 の2次元データとする。
| 3 | -2 | 4 | 1 | 0 | -3 |
| -2 | 1 | 0 | -2 | 3 | 4 |
| 1 | -3 | -2 | 2 | 1 | -1 |
| -4 | 0 | 3 | 2 | -1 | 2 |
これに以下に示す 3×3 のカーネルでストライド (1,1) の畳み込み (活性化関数なし) を適用するとする。
| 1 | -1 | 1 |
| -1 | 3 | -1 |
| 1 | -1 | 1 |
ただし、バイアスは以下とする。
| -7 |
カーネルが左上端のときには下図の赤枠の領域が対象となる。
| 3 | -2 | 4 | 1 | 0 | -3 |
| -2 | 1 | 0 | -2 | 3 | 4 |
| 1 | -3 | -2 | 2 | 1 | -1 |
| -4 | 0 | 3 | 2 | -1 | 2 |
領域のデータとカーネルの対応する値同士の積を足し合わせ、最後にバイアスを加算するので、以下の計算式となる。
総和 = 3*1 + (-2)*(-1) + 4*1
+ (-2)*(-1) + 1*3 + 0*(-1)
+ 1*1 + (-3)*(-1) + (-2)*1 + (-7) = 9
左上端のひとつ右にカーネルが来ると、下図の赤枠の領域が対象となる。
| 3 | -2 | 4 | 1 | 0 | -3 |
| -2 | 1 | 0 | -2 | 3 | 4 |
| 1 | -3 | -2 | 2 | 1 | -1 |
| -4 | 0 | 3 | 2 | -1 | 2 |
このとき、以下の計算式となる。
総和 = (-2)*1 + 4*(-1) + 1*1
+ 1*(-1) + 0*3 + (-2)*(-1)
+ (-3)*1 + (-2)*(-1) + 2*1 + (-7) = -10
以下、カーネルをデータ全体の範囲内でずらしていき、その結果、以下の 4×2 サイズの次層のデータが得られる。
| 9 | -10 | -16 | -2 |
| -19 | -14 | 5 | -1 |
なお、ストライド (1,1) の場合、畳み込み適用後のサイズは
横幅 = 元データ横幅 - カーネル横幅 + 1
縦高さ = 元データ縦高さ - カーネル縦高さ + 1
となる。
層間でデータの縦横サイズを変えたくない場合もある。その場合は パディング (padding) によって本来のデータの外側に余分のデータを補って計算させる。
カーネルが 3×3 の場合は、上下の外側に各1行分、左右の外側に各1列分のデータを補う。補うデータとしては 0 が利用されることが多く、0 パディング (zero padding) と言われる。
上例の 6×4 の元データに 0 パディングを行うと以下となる。
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 3 | -2 | 4 | 1 | 0 | -3 | 0 |
| 0 | -2 | 1 | 0 | -2 | 3 | 4 | 0 |
| 0 | 1 | -3 | -2 | 2 | 1 | -1 | 0 |
| 0 | -4 | 0 | 3 | 2 | -1 | 2 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
これに対して先ほどと同じ 3×3 のカーネルおよびバイアスを使って畳み込み (活性化関数なし) を適用すると以下となり、サイズは 6×4 で元データと変わらない。
| 7 | -23 | 5 | -3 | -6 | -17 |
| -23 | 9 | -10 | -16 | -2 | 7 |
| 6 | -19 | -14 | 5 | -1 | -15 |
| -23 | -4 | 1 | -6 | -14 | 2 |
得られた 6×4 サイズのデータに対し、今度は 2×2 の最大値プーリングを適用して、データサイズを縮小する。データの 2×2 領域ごとに最大値を代表として選ぶと、適用後は以下の 3×2 サイズのデータとなる。
| 9 | 5 | 7 |
| 6 | 5 | 2 |
また、同じ 6×4 サイズのデータに対し、2×2 の平均プーリングを適用すると、以下の 3×2 サイズのデータとなる。
| -7.5 | -6 | -4.5 |
| -10 | -3.5 | -7 |
※ 上例および下の演習では、計算を簡単にするためデータやカーネルおよびバイアスの各値を整数としているが、実際の問題に適用される CNN では多くの値が絶対値の小さい小数となっている。
CNNの途中の層が以下で示す 6×4 の2次元データとする。
| -4 | 2 | 0 | 1 | -3 | 2 |
| 1 | -2 | -3 | 1 | -4 | 0 |
| 3 | -1 | 2 | -2 | 0 | 4 |
| -2 | 4 | 1 | -3 | 2 | -1 |
これに以下に示す 3×3 のカーネルでストライド (1,1) の畳み込み (活性化関数なし) を適用するとする。
| -1 | 2 | -4 |
| 1 | -2 | 2 |
| -3 | 1 | -1 |
ただし、バイアスは以下とする。
| -3 |
Excelの表を利用して以下を順にまとめる。
- パディングなしで畳み込みを適用した場合の結果のデータを2次元表形式で示しなさい。
- 0 パディングによりデータのサイズを変えずに畳み込みを適用した場合の結果のデータを2次元表形式で示しなさい。
- 0 パディングの畳み込み後のデータに 2×2 の最大値プーリングを適用する。得られるデータを2次元表形式で示しなさい。
以下をMicrosoft Excelで作成し、PDFファイルとして保存し、授業Webページから提出しなさい。(ExcelでPDFに変換できなかった場合は、Excelファイル (拡張子 .xlsx) を提出しなさい)
- 先頭に「学籍番号・氏名」と「課題番号 課題名」
- 演習23 の 1 〜 3 を順にまとめる。
1.3.2 実際のCNNでの畳み込み
まず、今回の例および演習では触れられなかったが、畳み込みで使うカーネルの要素およびバイアスは重みパラメータであり、学習時の逆伝播の際に値が更新されていく。
今回の例および演習では、入力側は2次元データが1面のみで、カーネルも1個のみ、出力側の2次元データも1面のみであった。
しかし実際のCNNでは、2次元データ1面を チャネル (channel) として、典型的には、入力側も出力側も複数チャネルのデータとすることが多い。
その場合は、カーネルを「入力側チャネル数 × 出力側チャネル数」個およびバイアスを「出力側チャネル数」個用意し、各入力チャネルデータに対し、その入力チャネルおよび出力チャネルに対応するカーネルを作用させて畳み込みを行い出力チャネルごとの総和を求め、最後に出力側に対応するバイアス値を加えることによって値を求める。
多数のチャネルを用意することで、データについて、できるだけ多くの特徴を捉えられるようになることを狙いとしている。
実際、高い画像認識性能を持つCNNでは、畳み込みを行った後では多数のチャネルに画像のさまざまな特徴が反映されている。
その意味で、畳み込み層からの出力チャネルひとつひとつは 特徴マップ (feature map) と言われる。
パラメータ数について考慮すると、
入力側チャネル数が ci 、出力側チャネル数が co のとき、畳み込み層の重みパラメータの数は
となる。
カーネル要素数は固定された小さな数 (5x5カーネルでも25個) で、ci , co が大きくなるとパラメータも増大するが、それでも大きな2次元データに対して全結合で次の層を求める場合に比べると圧倒的にパラメータ数を抑えられる。
最後に、今回は活性化関数を使っていないが、実際のケースでは活性化関数も使われる場合が多い。畳み込み層では、通常、活性化関数として ReLU が使われる。
1.3.3 深層学習 (ディープラーニング) への発展
活性化関数に ReLU を使う、多くの畳み込み層・プーリング層を使うといった工夫により、かなりの多層になったニューラルネットワークを使った機械学習手法は 深層学習 または ディープラーニング (deep learning) と言われ、画像認識の分野や囲碁プログラム AlphaGo などゲーム強化の分野で大きな成果を挙げた。
深層学習 (ディープラーニング) は、現在でも盛んに、さまざまな広い分野の問題についての応用が図られている。
1.4 NNを使った機械学習の演習
CNNを使った画像認識等の演習はこの授業では実施しない。学科では、他科目で学習できる。
この授業の NN (ニューラルネットワーク) 演習では、層数の少ない全結合のみの順伝播型ニューラルネットワークを使って、機械学習の分野で定番の問題とされているアヤメの品種分類を学習させる。
アヤメの特性データとして、
- ガク片の長さ(cm)
- ガク片の幅(cm)
- 花びらの長さ(cm)
- 花びらの幅(cm)
という4つ一組のデータが 150 個あり、そのデータに対応したアヤメの品種として、ラベル値 150 個
| 値 | 品種 |
|---|---|
| 0 | セトナ (Iris-Setosa) |
| 1 | バーシクル (Iris-Versicolour) |
| 2 | バージニカ (Iris-Virginica) |
が用意されている。
全結合のみの順伝播型ニューラルネットワーク (中間層1層) を構築し、150組のデータのうち、何割かを訓練データとして学習させる。
訓練データ一式の1回の学習を エポック (epoch) というが、1エポックの学習だけでは十分に学習が進まないので繰り返し学習させる。
入力層はノード数 4 固定のベクトルで、アヤメの特性データを入れる。
中間層の活性化関数は ReLU とする。中間層のノード数は何通りか変えて、いい結果が得られるものを選ぶ。
出力層はノード数3固定のベクトルで、softmax活性化関数 を使って、0番ノードの値 p0 がセトナに、1番ノードの値 p1 がバーシクルに、2番ノードの値 p2 がバージニカに、それぞれ分類される確率を表す。活性化関数を通す前の 0, 1, 2 番ノードの値をそれぞれ v0, v1, v2 としたとき、
Σ pi = 1
の関係がある。(ここで exp は自然対数の底 e のべき乗を表す)
ネットワーク構造を下に示す。なお、①となっているノードからの矢印はバイアス値を、青色の部分は ReLU 活性化関数を、橙色の部分は softmax 活性化関数を、それぞれ示す。
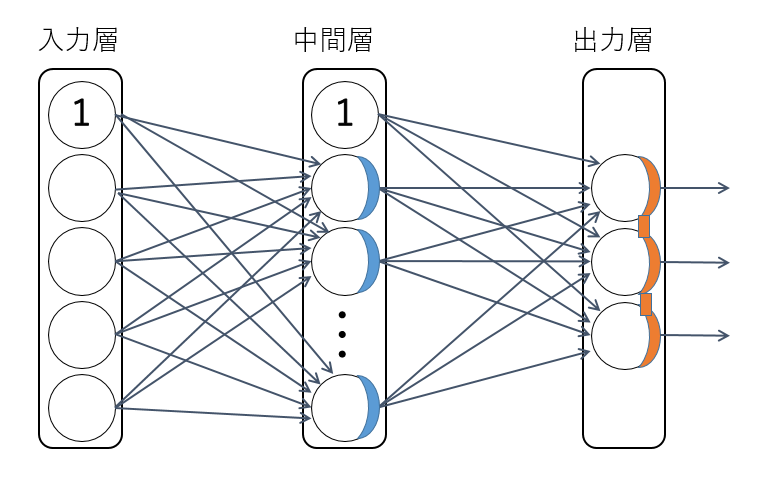
今回は分類問題なので、損失関数は下式で与えられる交差エントロピーを使う。
ここで、pi は softmax の i 番目の出力値、ti は訓練データの分類における i 番目の値である。今回のアヤメのデータは品種が完全に分類できているので、ti は正解の分類値のときのみ 1 で、他は 0 となる。このとき、交差エントロピーは
となる。
演習のプログラムでは、各エポック終了時に、訓練の損失関数の平均値と訓練データの正解率およびテストデータの正解率を示している。
ただし、今回のサンプルではデータ数が全体でも 150 と少なく、それをさらに訓練データとテストデータに分けているので、確率的なバラつきが非常に大きく、少なくとも10回以上やって平均の値を見るようにしなければならない。
テストデータは訓練には使われていないが、今回のニューラルネットワークが全体のデータに対する 汎化 (generalization) 能力を発揮できれば、テストデータでも高い正解率が得られるはずである。
訓練データの結果に比べてテストデータの結果がかなり悪いとき、過学習 (overfitting) が起こっているといわれ、訓練データの細かい特徴に引っ張られて学習がうまく進んでいないとされる。
過学習になった例
うまく学習が進んだ例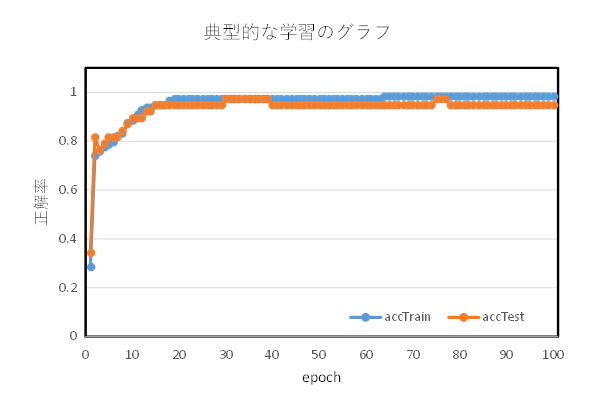
Teams「人工知能」チームの「ファイル」の「NN」フォルダにある、アヤメ品種分類プログラムのソースファイル IrisClassify.java をダウンロードし、サクラエディタ等で開いてみなさい。
上記はJavaの単一ソースファイルのみのプログラムで、使用している環境のJavaのJDKのバージョンが 18 以降であれば、
java IrisClassify.javaで実行できる。
※ Javaのバージョンが古い場合や、エンコードの問題でエラーや文字化けになる場合は、javac コマンドで -encoding UTF-8 オプションでソースファイルのエンコードを指定してコンパイルし、java コマンドで実行する。
ソースを変更するごとにコンパイルをする必要があるので注意。
javac -encoding UTF-8 IrisClassify.javajava IrisClassify
1. 中間層のノード数を
- 小さい数 (3 程度)
- 中間 (20 程度)
- 大きい数 (100 程度)
に設定して実行し、学習の進み具合、分類の正解率の推移を調べなさい。 出力をファイルにリダイレクトして保存し、Excelに読み込ませて、epoch を横軸・accTrain および accTest を縦軸にしたグラフを作ってみるとよい。 なお、accTrain は訓練データの正解率、accTest はテストデータの正解率を表している。
確率的なバラつきが非常に大きいので、各設定で少なくとも10回は実行して平均の値を見て一番良いと思われる値を採用すること。下の 2, 3 でも同様に各設定で少なくとも10回は実行すること。
2. 以下では、上で適切と思われた中間層ノード数の下で行なう。
上では、訓練データの全体に対する割合は
であったが、この割合を
に設定し、学習の進み具合、分類の正解率の推移を調べなさい。
accTrain と accTest のズレに注目すること。
多数回(10回以上)実行し、どのような傾向があるかを見出し、その理由を考察し、問題点を指摘しなさい。
同様に、訓練データの全体に対する割合を
に設定して多数回(10回以上)実行し、どのような問題に陥る傾向があるかを見出し、その理由を考察しなさい。
3. 訓練データの割合を元に戻した上で、学習率を
- 大きい値 (0.4 程度)
- 少し小さ目 (0.01 程度)
- もう少し小さ目 (0.001 程度)
- すごく小さい値 (1e-5 程度)
に設定して、それぞれ多数回(10回以上)実行し、学習の進み具合、分類の正解率の推移を調べなさい。
以下をMicrosoft Excelで作成し、PDFファイルとして保存し、授業Webページから提出しなさい。(ExcelでPDFに変換できなかった場合は、Excelファイル (拡張子 .xlsx) を提出しなさい)
- 先頭に「学籍番号・氏名」と「課題番号 課題名」
- 演習24 の 1 で、中間層のノード数がそれぞれ小さい数、中間、大きい数のときの100エポック後の accTrain, accTest の平均値を示し、どれを選択すべきかを、その理由を含めて説明する。
- 同じく 2 で、訓練データの全体に対する割合が 0.95, 元の設定値 0.75, 0.05 それぞれのときの100エポック後の accTrain, accTest の平均値を示し、どういう理由で学習が進まない傾向にあるかを説明する。
- 同じく 3 で、学習率を大きい値、少し小さ目、もう少し小さ目、すごく小さい値にそれぞれ設定したときの100エポック後の accTrain, accTest の平均値を示し、どの辺りの値を選択すべきかを、その理由を含めて説明する。
1.5 ディープラーニングのライブラリの利用
上の演習では、中間層1層のニューラルネットワークを一から実装したプログラムを使用した。しかし、実際に大きなデータに機械学習を適用する場面では、ニューラルネットワークの構造や最適化手法を色々変えてよい結果の出るものを選びたい。
そういう場合に一からプログラムを記述していくやり方だと効率が悪すぎる。
ニューラルネットワークにはフリーで使えるライブラリまたはフレームワークが非常に多く存在し、GPU (Graphics Processing Unit) の利用に対応しディープラーニングまで可能な優れたものが多く公開され利用されている。代表的なものをいくつか示す。
※ GPU (Graphics Processing Unit) は元々はコンピュータ画面の画像処理用プロセッサだが、並列処理能力に優れ、そのために並列化しやすいニューラルネットワークの計算で非常に優れた性能を示すため、本格的な深層学習 (ディープラーニング) では不可欠なものとなっている。
- Chainer (開発終了)
- TensorFlow
- Keras
- PyTorch
これらはインターネットからダウンロードできるので、今後卒業研究でニューラルネットワークによる機械学習を行う場合などに利用するとよい。
先の演習でやったアヤメの特性データの機械学習を、Keras (正確には TensorFlow に組み込まれている Keras) を使って書き直して動作させてみる。
多くのディープラーニングライブラリはプログラミング言語 Python で使うようになっており、Kerasを用いた機械学習も Python のプログラムになる。
1.5.1 環境の準備
※ 自宅PC・ノートPCなどの場合
Python 環境が用意されていない場合は、公式サイト Python.org からダウンロードして Python をインストールする。
2025/12/6 時点の最新版 Python 3.14.2 をインストールしても、それに対応した TensorFlow パッケージが用意されていないので、数バージョン前の Python をインストールする。
例えば、
にある
の
をダウンロードする。(ただし、上リンクは64ビットWindowsの人用。32ビットWindows など、他環境の人は該当するリンクを探すこと)
ダウンロードしたファイルを実行しインストールする。その際、
にチェックを入れること。(上記 x.x には Python のバージョンが入る)
Pythonを自分で使うだけなら、「Install launcher for all users」はチェックがなくてもよい。
設定ができたら
からインストールできる。
Python.org で Python をインストールした場合は、ほとんどのライブラリがインストールされていない。下記プログラムで必要な scikit-learn (sklearn) パッケージも入っていない
そこで、Pythonのインストール後に、PowerShell またはコマンドプロンプトを新たに起動し、以下のコマンドでインストールする。
pip install scikit-learnTensorFlow も入っていないので、以下のコマンドでインストールする。
pip install tensorflow以上で、下記演習のプログラムが動作する環境が用意される。
※ Google Colab を使った TensorFlow プログラムの使い方
演習室PCでは、手軽に Tensorflow のプログラムを実行する方法として、「ブラウザから Python を実行できるサービス」である Google Colab を用いた実行方法を示す。
自前のPCでも Python や TensorFlow をインストールしないままプログラムが動かせるので、こちらの方法が手軽である。
ただし、Googleアカウントが必要となる。
Googleアカウントをまだ持っていない人は、
に入って必要事項を登録し、アカウントを作成する。
Google アカウントを所持したら、
に入り、そのアカウントで Google Colab に「ログイン」する。
場合により、アカウント登録の際に入れた番号のスマートフォンなどに確認メッセージが送られるので対応すること。
ログインできたら、
「ドライブの新しいノートブック」を選択
Untitled数字.ipynb というノートブックが開く。(数字は順に変わっていく)
とある部分に直接コードを入れていくか、または、別ファイルで Python ソースプログラムを作っておきコピー&ペーストする。
コードの左側の ▶ をクリックしてプログラムを実行する。
※ 演習室PCでの今回のプログラムの実行方法例 (準備に時間がかかる。毎回インストールが必要)
コマンドプロンプトを起動する。
まず、以下のコマンドでPythonのインストールを確認する。
py -0p
出力から、
C:\Users\fit-user\AppData\Local\Programs\Python
以下にインストールされているPythonがデフォルトとなっていることが分かる。このPythonに対し、以下のコマンドを順に実行し、scikit-learn と tensorflow をインストールする。
py -m pip install scikit-learn
py -m pip install tensorflow
インストールが終われば、今回のPythonプログラムのソースファイル (UTF-8エンコーディング) が例えば iris.py だとすると、そのファイルのあるフォルダに cd コマンドで移動の上、以下のコマンドで実行できる。
py iris.py※ PC演習室のパソコンにインストールをした場合は再起動するとその内容は消えるので、毎回 scikit-lean と tensorflow をインストールし直してプログラムを動作させる必要がある。PC演習室の場合は上記の Google Colab を使う方法が手軽である。
※ 演習室PCでの TensorFlow の使い方
大学 PC演習室のPCには Anaconda がインストールされている。 スタートメニューから
を選び起動する。
まず、
pip listというコマンドで、演習室の Anaconda 環境にインストールされているパッケージの一覧を出力し、scikit-learn パッケージおよび tensorflow パッケージが入っているかどうか調べる。
パッケージが入っていなかった場合は、以下のコマンドで自分用に scikit-learn と tensorflow をインストールして使用する。
pip install --user scikit-learn tensorflow※
【補足】
下記演習プログラムを実行してみて
RuntimeError: module compiled against API version 0xf but this version of numpy is 0xe
のような numpy のバージョンが違うエラーが出て正常に実行されない場合、プロンプトから
pip install numpy --upgrade
を入れて numpy のアップグレードをする必要がある。上でも動作しないなら
pip install numpy --upgrade --ignore-installed
を試す。
Pythonプログラムのファイルは拡張子 py のテキストファイルとする。
サクラエディタ等のテキストファイルエディタを開きコードを入力していく。まず、ファイルの先頭でTensorFlowおよびKerasの利用のため以下の import をする。
import tensorflow as tf from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Input, Dense from tensorflow.keras import optimizers
TensorFlowのバージョンが 2.0 から 2.3 の場合は、追加で、下記のTensorFlow バージョン 1 用のプログラムをバージョン 2 の下で動作させるための設定を入れる。
※ TensorFlow バージョン2系でも、2.4.0 以降は下記コードは不要。
tf.compat.v1.disable_eager_execution()
また、アヤメデータの読み込みと訓練データ・テストデータの分離のため以下も import する。
from sklearn import datasets from sklearn.model_selection import train_test_split
実際のデータの読み込みと訓練データ・テストデータの分離は以下のコードとなる。ここで、train_size に設定する値は全体のデータに対する訓練データの割合であり、適宜、値を設定する。
iris = datasets.load_iris()
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, train_size=0.75)
以下で、ニューラルネットワークのモデル構築をする。順伝播型ニューラルネットワークは、Kerasでは以下のように手軽にモデル構築できる。
model = Sequential([ 入力層の定義 , 中間層1の定義 , ・・・ ここに必要なだけ中間層を定義 (コンマ区切り) ・・・ 中間層n→出力層の定義 ])
まず、「入力層の定義」では、Input(shape=データ形状のタプル) によって、入力データの型 (データがどういうサイズの何次元のものか) を指定する。今回の問題では、入力データは4つ組の集まりなので、データ一組分の型として
Input(shape=(4,)),
と指定する。これにより、入力データは (データの個数, 4) の型となる。
今回の問題では、層と層の間はすべて全結合となる。Kerasでは、全結合を Dense で記述する。
Dense では、最初のパラメータで次の層のノード数を指定する。
また、activation によって活性化関数を指定する。
今回の問題では、最後の出力層の活性化関数は softmax 関数で、activation=tf.nn.softmax で指定できる。それ以外の中間層の活性化関数は ReLU で、activation=tf.nn.relu で指定できる。
以上をまとめると、「入力層の定義」および「中間層1の定義」は
Input(shape=(4,)),
Dense(中間層のノード数, activation=tf.nn.relu),
の形となる。「中間層のノード数」は適宜設定する。
次に、「中間層n→出力層」は
Dense(3, activation=tf.nn.softmax)
となる。今回の問題では出力は3分類のsoftmaxなので、最初に3を指定している。
「入力層」、「中間層1」と「中間層n→出力層」だけだと、全結合の中間層1層・出力層3分類の softmax という単純なネットワーク構造となる。間に Dense を追加することで、容易に、中間層の数を増やせる。
続いて、ニューラルネットワークの学習 (最適化) 方法として SGD を指定する。ここでは、学習率を表す learning_rate パラメータを適切な値に設定する。
分類問題なので、loss パラメータで指定する損失関数は交差エントロピーとする。今回のように多クラス分類問題の正解データ(ラベル)がカテゴリ番号で与えられている場合は sparse_categorical_crossentropy を指定する。
また、評価指標として accuracy (正答率) を指定する。
opt= optimizers.SGD(learning_rate=学習率, momentum=0.0)
model.compile(loss='sparse_categorical_crossentropy', optimizer=opt, metrics=['accuracy'])
以下のコードで、モデル構造の簡易出力をする。重みパラメータの数が表示されるのでチェックしておく。
model.summary()
訓練データ x_train, y_train を使って fit することによって多数エポック回分学習を行わせる。必要ならエポック数 epochs=100 を大きくしても構わない。
model.fit(x_train, y_train, epochs=100)
テストデータ x_test, y_test を使って evaluate することによって正答率を調べ、表示させる。
score = model.evaluate(x_test, y_test, batch_size=1)
print('正答率(accuracy) = ', score[1], sep='')
演習24 で一番うまく学習が進んだと思われる各種設定を使って上記の一連のコードを入れたファイル (中間層1層) を作り保存する。ファイル名は .py で終わる名前とし、保存のエンコーディングは UTF-8 を指定すること。
Python.org のPython環境の場合、PowerShell または コマンドプロンプトを起動する。
cd コマンドで保存したファイルのあるディレクトリに移動した上で
python ファイル名
で実行し、accuracy の変化によって学習の進み方を見る。
Google Colabでは、▶ をクリックして実行する。
演習24の結果と同程度の結果が得られればよい。
多数回(10回以上)実行し、正答率の平均を示しなさい。
深層学習用フレームワークを使うと、ネットワーク構造を容易に変更して学習を試すことができる。下の演習では、中間層を追加してみる。
ネットーワーク構造を中間層2層に変えて、それに伴い各種設定を変え、うまく学習が進むように調整して実行してみなさい。
同様に、ネットーワーク構造を中間層3層に変えて、それに伴い各種設定を変え、うまく学習が進むように調整して実行してみなさい。
それぞれ、多数回(10回以上)実行し、正答率の平均を示しなさい。
層が多くなるとパラメータ数が増加する。プログラムの出力の最初でネットワーク構造が表示されるが、パラメータ数も表示されるので、確認し、あまり大きくなり過ぎないようにする。この演習では、パラメータの合計数が数百に収まるよう中間層のノード数を調整する必要がある。
以下をMicrosoft Excel等で作成し、PDFファイルとして保存し、授業Webページから提出しなさい。(ExcelでPDFに変換できなかった場合は、Excelファイル (拡張子 .xlsx) を提出しなさい)