コンピュータゲーム研究の現状・動向、完全情報二人ゲームの探索法

1.1 完全情報ゲームと不完全情報ゲーム

完全情報ゲーム

• プレーヤはすべてのゲーム状態を把握できる
• 囲碁、将棋、バックギャモンなど

不完全情報ゲーム

• プレーヤに隠されたゲーム状態がある
• 情報集合(プレーヤにとって識別できない可能なゲーム状態の集合) が複数要素を持つ
• ほとんどのカードゲーム、麻雀、軍艦ゲーム、軍人将棋、衝立将棋、DI将棋など

1.2 思考型対戦ゲームの分類と研究の動向

完全情報二人ゲーム

• チェス、将棋を始め盛んに研究され、人間を超えるようなプログラムが作られている
• 基本手法は探索。効率化が問題

不完全情報二人ゲーム

ブリッジ、ポーカーなどカードゲームを中心に研究されている。まだまだ課題が多い。

多人数ゲーム

プレーヤ同士の強調・裏切りなどがあり難しい。ゲーム理論的な解析はされているが、コンピュータプレーヤは中々本格的に研究できない。

1.3 完全情報二人ゲーム研究の現状

チェス

• 人間チャンピオンを破る (Deep Blue vs. Kasparov, 3.5-2.5, 1997)
• 専用ハードウェアによる高速先読み
• 終盤データベースによる終盤の完全プレイ

将棋

• 2010年代前半まででプロトップクラスを既に超えている。
• 【問題点】序盤・中盤の、長い手数の駒組み構想が甘い。人間が見つけたトラップ手順にはまりやすい。

囲碁

• 調べる局面数が爆発的に多いので、コンピュータ的に難しい。
• ゆっくりながらも進歩していた。
• モンテカルロ法が成功し、強さが格段にアップし、トッププログラムは4子局でプロ棋士に勝つなど、棋力はアマ三、四段程度になっていた。
• しかし、人間プロレベルに達するのはしばらくかかると思われていた。
• 2016年から2017年に AlphaGo が欧州のトッププロ・韓国のトッププロ・中国のトッププロ (世界トップレベル) を打ち負かした。人間プロを越えたと考えられる。

1.4 完全情報二人ゲームの手法

• 探索空間を限定的に探索し、未展開節点を評価関数によって点数づける (ミニマックス木)

• ミニマックス探索
• αβ探索
• PVS, ウィンドウ探索, NegaScout など改良された探索法
• 実現確率探索
• 高速な終盤探索 (証明数探索)
• データベース、ハッシュ表の有効利用

1.4.1 ミニマックス木 (minimax tree)

調べたい状態から可能選択をすべて考えていくとゲーム木が構成される。下に深さ3のゲーム木の例を示す。

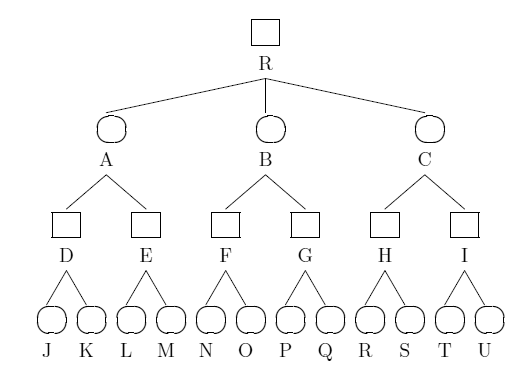図1  ゲーム木の例

ゲーム木はすべての枝が末端節点 (ゲームが終了し結果が出た状態) に至るまで展開される。上図の深さ3の各節点の下にも後続節点が続いていると考えられる。

探索空間が大きいときはすべてを調べ尽くすのは不可能なため、ゲーム木で表される探索空間を限定的に展開し、未展開節点を評価関数 (evaluation function) によって点数づける。これをミニマックス木と言う。
限定的な展開として、最もシンプルなアルゴリズムでは、探索深さ限界を決め一定深さになったら展開を止め状態を点数付けする手法が利用される。

下図は深さ3を探索限界として評価関数によって点数付けした場合のミニマックス木の例である。

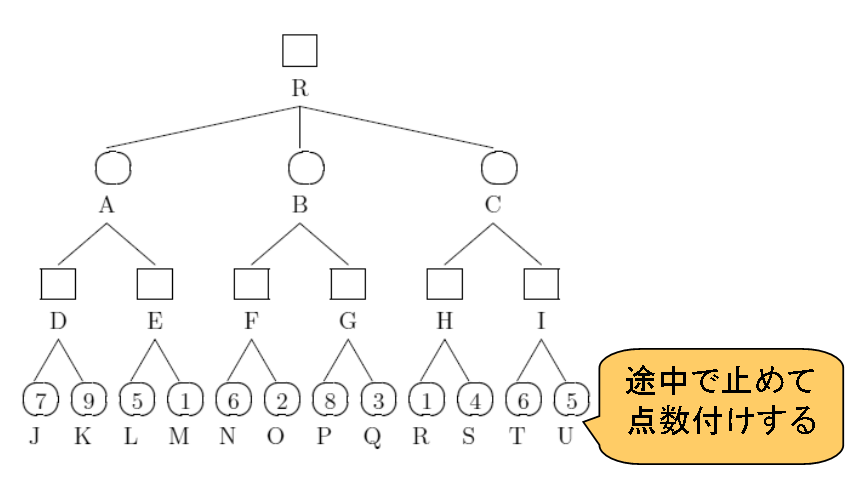図2  ミニマックス木の例

途中の状態で探索を打ち切るため評価関数のできが強さに直結する。 極端な話極めて正確な評価関数があれば、探索は必要なく、選択候補の中で最も高い評価関数の値を持つものを選べばよい。

しかし現実には正確な評価関数を作ることは困難である。 評価関数はアルゴリズムで確固たるものが作れるわけではなく、ヒューリスティック (発見的) な手法により作成される。結局、個々のゲーム種の性質に応じて調整するしかない。 いろいろな要素の線形結合式で表されることが多く、パラメータは人手で細かく調整されるか、もしくはコンピュータの自動学習により調整される。
ニューラルネットによる非線形要素を含み得る評価関数の学習・調整も行われている。

※※※※※
探索空間が大きくないときは調べつくすことができる。その場合の評価関数は単に末端節点のゲームの結果を点数化したものでよい。
※※※※※

1.4.2 ミニマックス探索 (minimax search)

未展開節点から

自分の番 (MAX節点) なら一番点数の高いものを選ぶ

相手の番 (MIN節点) なら一番点数の低いものを選ぶ

ことにより、上の節点を点数化していき

根節点で一番点数の高くなるもの

を選ぶ。

(例)

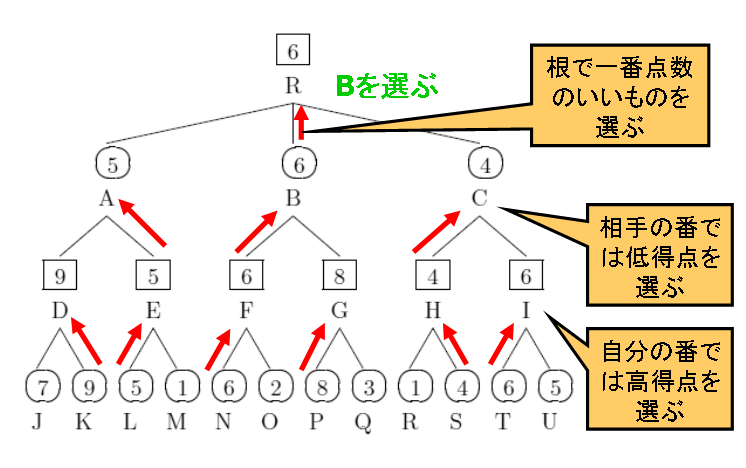図3  ミニマックス探索の例

1.4.3 αβ探索 (alpha-beta search)

ミニマックス探索における無駄な探索を省き、より効率的にした探索法で、すべてのコンピュータゲームプログラムの基礎となっている。
探索は下限値を表すα値と上限値を表すβ値によって制御される。

αカット

MIN節点の探索中、ある子MAX節点でα値より小さい評価値が見つかった場合、以降の節点は何であろうと無関係なので、探索をカットし現在の評価値を返す。

βカット

MAX節点の探索中、ある子MIN節点でβ値より大きい評価値が見つかった場合、以降の節点は何であろうと無関係なので、探索をカットし現在の評価値を返す。

(例)

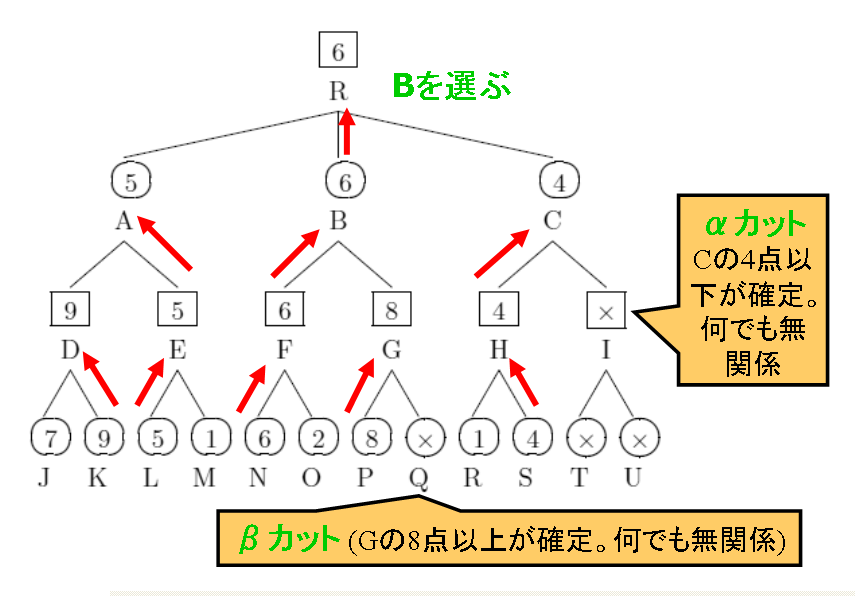図4  αβ探索の例

1.4.4 実現確率探索

• 選択を種類分けし、多数のゲーム記録を基に選ばれる確率を算定

• ゲーム木を深さ一定で調べるのではなく、確率の閾値を決めゲーム木を展開・評価し選択する。

• 確率の大きい選択は深く、確率の小さい選択は浅く展開する。

(例)

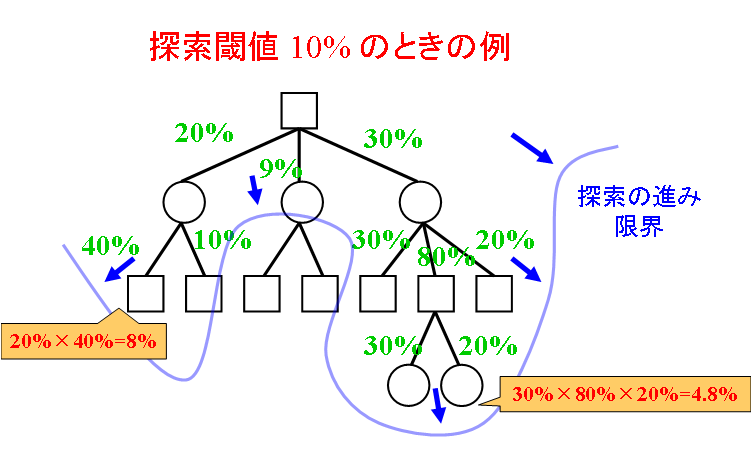図5  実現確率探索の例

1.5 コンピュータに対する誤認識

• 米長邦雄 (将棋プロ、永世棋聖)
  「強者は泥沼で戦う」 (1980年頃)

• 1997 年頃までのプロ将棋界の考え方
  コンピュータのように序盤ばかり研究してもダメ。真の力は泥沼の戦いで発揮される。

• 確かに昔のコンピュータ将棋は序盤定跡を外れるととんでもなく弱かった。

• しかし現状は…
  型にはまった戦い方をするのは人間
  泥沼に強いのはコンピュータ

1.6 チェス、将棋の研究からわかること

• 探索が人間の思考・直感を陵駕
• 金沢 伸一郎 (将棋ソフトの作者) (2000年発行「コンピュータ将棋の進歩3」から)

  「思考ゲームにおける直感的な手というのは，その多くは神秘的なものではなく，それを指した(打った)人が単に言語化ができていないだけで，無自覚の内に高速な思考をしているのだと考えているので，コンピュータらしく，その直感といわれている人間の能力を上回るほど読んでしまえばいいのである。」

  現実は、金沢氏の予想通りになっていった。

1.7 チェスの状況

1997年 人間チャンピオンを破って以降の動向

• アドバンスト・チェス の登場
  人間がコンピュータを助けにして対局する

1.8 「人間 vs. コンピュータ」の現状・展望

将棋

将棋連盟が認めた「プロ棋士 vs. コンピュータ」の対局の歴史

• 2007.3.21 コンピュータ将棋 Bonanza vs. 渡辺竜王
  タイトル保持者とコンピュータ将棋との平手対局として注目を浴びた。
  持ち時間: 各2時間 (チェスクロック使用)
  結果は渡辺竜王の勝ち。渡辺竜王によると自分が不利な局面もあったとのこと。コンピュータがプロ棋士にとってもあなどれなくなったことが認められた。

• 2010.4.2 情報処理学会が将棋連盟に挑戦状
  将棋連盟が受けて立ち、以降、プロ棋士対コンピュータの対局が行われていく段取りとなった。

• 2010.10.11 清水市代女流王将 vs. あから2010
  持ち時間: 各3時間(チェスクロック使用) 切れたら1分

  ※ あから2010
  4プログラム 激指、GPS将棋、Bonanza、YSS の多数決制

  結果は86手でコンピュータ側の勝ち。
  

• 2012.1.14 第1回電王戦

  コンピュータ将棋(ボンクラーズ) vs. 米長邦雄永世棋聖
  持ち時間: 各3時間で、1分未満はカウントしない

  米長氏は2003年12月に引退した元トップレベルのプロ棋士
  コンピュータ対策に2手目6二玉から争点を作らず盛り上がる作戦を用いたが、結果は113手でコンピュータの勝ち

• 2013.3.23 - 4.20 第2回電王戦

  持ち時間各4時間(1分未満切り捨て)、時間切れ後は1手1分。
  先後は振り駒で決定。

  ○阿部光瑠四段 vs ●習甦 (しゅうそ)
  ●佐藤慎一四段 vs ○ponanza
  ●船江恒平五段 vs ○ツツカナ
  △塚田泰明九段 vs △Puella α    持将棋引き分け
  ●三浦弘行八段 vs ○GPS将棋   

  若手の強豪棋士・A級棋士(トッププロ)三浦八段を含む5人で対戦したが、
  結果はプロ棋士の1勝3敗1分。
  特に三浦八段が負けたことは重要。

  コンピュータ将棋が事実上プロレベルかあるいはそれ以上であることが分かった。

• 2014.3.15 - 4.12 第3回電王戦

  コンピュータ側は主催者の用意する統一パソコン上でプログラムを動作させる。
  これにより、必ずしもその時点での最高のコンピュータプログラムとは言えなくなっている点には注意しておく必要がある。

  持ち時間はチェスクロック方式の各5時間、切れたら1分将棋。
  コンピュータは Core i7 Extreme4960X EE 3.6GHz 6コア、メモリ 16GB。

  ●菅井竜也五段 vs ○習甦 (しゅうそ)
  ●佐藤紳哉六段 vs ○やねうら王
  ○豊島将之七段 vs ●YSS
  ●森下卓九段 vs ○ツツカナ
  ●屋敷伸之九段 vs ○ponanza
  

  この結果を素直に見れば、一般パソコンのソフトに一流プロが敗れており、第2回の結果と合わせて、少なくとも、将棋ソフトがタイトルを持っていない棋士たちよりも強くなったことが言える。小谷氏の分析では、トップソフトとプロ棋士の事実上のトップである羽生名人とが拮抗するレベルにあるのではないかと考察している。

  なお、ソフトの着手には、デンソーウェーブがロボットアーム VS-060 をベースに改造した「電王手くん」が利用された。

• 2015.3.14 - 4.11 電王戦FINAL

  第3回と同様、統一パソコン上でプログラムを動作させる。
  コンピュータは Core i7 Extreme5960X EE 3.0GHz 8コア、メモリ 64GB。

  持ち時間は各5時間・秒読み1分。

  ○斎藤慎太郎五段 vs ●Apery
  ○永瀬拓矢六段 vs ●Selene   角不成の王手を認識できず反則負け
  ●稲葉陽七段 vs ○やねうら王
  ●村山慈明七段 vs ○ponanza
  ○阿久津主税八段 vs ●AWAKE   角を捕獲される手順に入ったところでAWAKE作者の判断で投了
  

  結果はプロの3勝2敗であるが、勝った3局は貸し出されたソフトを研究し、弱点あるいはバグを見つけて利用した結果であり、プロが正攻法で勝ったとは言いにくい。

  なお、ソフトの着手は、医薬・医療用ロボットを改造し、「電王手くん」ではできなかった駒の成動作もできるようになった「電王手さん」が利用された。

• 2016.4.9-10, 2016.5.21-22 第1期電王戦

  2番勝負
  2日制。持ち時間 各8時間 (チェスクロック使用)・秒読み 1分

  ○ponanza vs ●山崎隆之八段
  ●山崎隆之八段 vs ○ponanza

  第3回将棋電王トーナメントの優勝ソフト ponanza が 2勝0敗

• 2017.4.1, 2017.5.20 第2期電王戦

  2番勝負
  1日制。持ち時間 各5時間 (チェスクロック使用)・秒読み 1分

  ○ponanza vs ●佐藤天彦名人
  ●佐藤天彦名人 vs ○ponanza

  第4回将棋電王トーナメントの優勝ソフト ponanza が 2勝0敗

  名人が敗れ、将棋での「人間 vs. コンピュータ」はコンピュータ将棋の勝利で決着したと言ってよい。

囲碁

• モンテカルロ法が注目される以前はプロレベルには遠かったが、モンテカルロ法の利用で格段に強くなった。

• 2012.3.17 コンピュータ囲碁(Zen) vs. 武宮正樹九段
  中国ルール。持ち時間:30分、切れたら一手30秒。置き碁でプロにハンデ
  5子局: Zenの10点勝ち
  4子局: Zenの19点勝ち

  武宮正樹九段はトップレベルのプロ棋士。
  Zen はトップレベルのプログラムで、モンテカルロ法を採用している。

• 2013.3.20 第1回電聖戦

  日本ルール置碁。コンピュータ側の4子局。持ち時間30分、切れたら1手30秒。

  Zen vs 石田芳夫 二十四世本因坊 (中押し勝ち)
  Crazy Stone (3目勝ち) vs 石田芳夫 二十四世本因坊

  Zen は上記ソフトだが、約1年進展したものである。
  Crazy Stoneは、2000年代後半に初めてモンテカルロ木探索を実装して成果をあげたプログラムで、その後も発展を続けている。
  Crazy Stoneについては「アマ六段くらいの力は十分ある。ただ、プロレベルにはまだまだ」という石田プロのコメントがある。

  電聖戦は、2013年から少なくとも5年間は定期的に開催される予定。

• 2014.3.21 第2回電聖戦

  日本ルール置碁。コンピュータ側の4子局。持ち時間30分、切れたら1手30秒。

  依田紀基九段 vs Crazy Stone (2目半勝ち)
  依田紀基九段 (中押し勝ち) vs Zen

• 2015.3.17 第3回電聖戦

  日本ルール置碁。コンピュータ側に4子または3子のハンデ。持ち時間30分、切れたら1手30秒。

  二十五世本因坊治勲 vs Dolbaram ハンデ:4子 (中押し勝ち)
  二十五世本因坊治勲 (中押し勝ち) vs Crazy Stone ハンデ:3子
• AlphaGo の衝撃
  • 2015年10月、ヨーロッパ王者でプロ二段のファン・フイ を 5-0 で破った。
  • 2016年3月、数多くの世界戦優勝経験のある韓国プロ棋士 イ・セドル 九段と5回戦い、大方の予想を覆し、4勝1敗と圧倒した。
  • 2017年5月には、世界最強とされる中国の柯潔 (か けつ) 九段と3回対戦し、3勝0敗と圧倒した。
  • AlphaGo は2016年の時点で人間トップを超えたと判断せざるを得ない。
  特徴
  • Google が買収した DeepMind 社の深層強化学習技術を囲碁に適用して成功
  • ニューラルネットによる深層学習 (deep learning) で局面評価を学習
    最初は、人間上級者の棋譜から3000万手を訓練データとして入力し学習し、
    次に、強化学習の一種Q学習と深層学習を組合わせ、自己対戦によって評価精度を高めた
  • モンテカルロ木探索を利用

1.9 まとめ

• コンピュータ将棋は2010年代前半で実質上人間トップレベルを超えた。コンピュータ囲碁でも2016年に人間トップレベルを超えたと考えられる。

• 人間がコンピュータに負けても、そのゲームは終わらない。
  コンピュータをいい研究手段にするなど、協調して発展していく。

• 「一個の人間対コンピュータ」でなく「人類の歴史 対 コンピュータ」は残る課題。
  コンピュータによる定跡や新戦法の確立への期待